1.0 Introduction¶
This post contains a derivation of a recurrence relation that can be used to calculate $\pi$. While it's not useful for the purpose of calculating to any decimal place imaginable, what's notable is that it only uses the Pythagorean thereom and should therefore be easy to follow. Unsurprisingly, the recurrence relation is neither original nor unique because it falls under the category of using polygons to compute $\pi$ (attributed to Archimedes). At the end of the notebook, the derived recurrence relation is implemented in code and run.
There is more than one way to use polygons in the computation of $\pi$. One could follow Archimedes' proof, which uses a theorem from Euclid's Elements. There are other discussions that make use of trigonometric functions. Of course, one could just use the Pythagorean theorem by reducing the n-sided polygons to right triangles, as done here.
I went through a few pages of google search results and found similar posts. (I posted this anyway because it was fun and mainly an excuse to create an IPython notebook.) The first link's code can achieve a much larger decimal place than that shown here because the author used a specialized decimal type instead of the default float type available in Python.
A good historical account of $\pi$ that I found while briefly searching is found here.
2.0 Problem set up¶
Consider one quarter of a circle with arbitrary radius, $r$, between $0$ and $90$ degrees. The below will mathematically describe the outer perimeter of many triangles drawn inside this region. The outer perimeter is composed of the triangles whose hypotneuses are closest to the circle's arc. The quantity of triangles drawn will be proportional to an integer index, $n$. All variables make reference to $n$ via a subscript.
Variable definitions¶
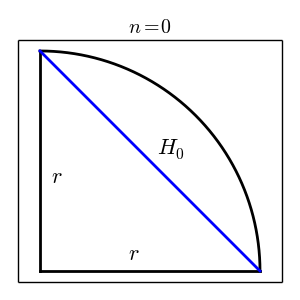
$r$ is the radius.
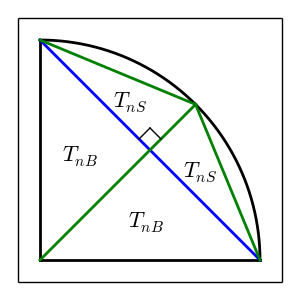
$T_n$ refers to any right triangle newly established at the $n$-th iteration.
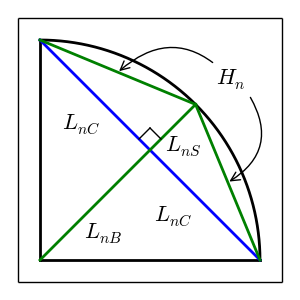
$L_n$ refers to any right triangle's leg.
$H_n$ refers to the hypotneuse of any small triangle ($T_{nS}$) that composes a portion of the outer perimeter.
$P_n$ is the outer perimeter.
Subscript meanings¶
Subscripts $B$ and $S$ refer to any big and small triangles, respectively.
$L_{nB}$ indicates a leg that is unique to $T_{nB}$.
$L_{nS}$ indicates a leg that is unique to $T_{nS}$.
$L_{nC}$ indicates a leg that is common to $T_{nB}$ and $T_{nS}$.
Below are explanatory images that indicate most of the above variables. They are for $n = 1$, and the procedure to arrive at the drawn line segments is outlined in the following subsections. The first figure indicates triangles, and the second figure indicates line segment lengths. Omitted from the second figure are the radius labels (the radii are at $0^o$, $45^o$, and $90^o$). The figures are an attempt to convey that there are two sets (big/small) of identical triangles at each iteration, and that by calculating the properties of one triangle in each set, all other triangles' properties are known.
Blue lines always correspond to refinements made at the previous iteration. Green lines are the new refinements made at the current iteration. This combination of line segments produces the set of $T_{nB}$ and $T_{nS}$ at iteration $n$.
3.0 Analysis¶
3.1 Analysis for n = 0¶
Inside the starting region a right triangle is created by connecting points $(0, r)$ and $(r, 0)$. The hypotneuse can be easily calculated by the Pythagorean thereom, and for $n=0$ the hypotneuse happens to be equal to the outer perimeter.
3.2 Analysis for n = 1¶
The previous right triangle's hypotneuse ($H_0$) is bisected by a line from the origin to the circle's perimeter at an angle exactly halfway between the legs (or catheti) of $T_0$. This action creates four new right triangles since the hypotneuse of $T_0$ forms a right angle with the bisecting line. These new triangles are two of $T_{1B}$ and two of $T_{1S}$.
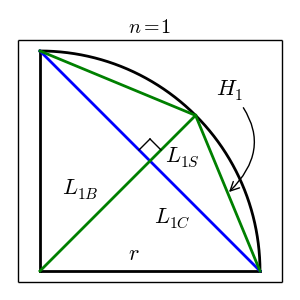
Since the hypotneuse of $T_0$ has been bisected, the leg that is common to any $T_{1B}$, $T_{1S}$ pair is known (this is $L_{1C}$). The hypotneuse of $T_{1B}$ is known because it is just $T_0$'s leg, $r$. Therefore, we can solve for the missing leg, $L_{1B}$.
$$ \begin{aligned} L_{1C} &= \frac{H_0}{2} \\ L_{1B} &= \sqrt{r^2 - L_{1C}^2} \end{aligned} $$The line segment labeled $L_{1S}$ is just the radius minus $L_{1B}$. This permits calculation of $H_1$, which is the hypotneuse of the small triangle $T_{1S}$.
$$ \begin{aligned} L_{1S} &= r - L_{1B} \\ H_1 &= \sqrt{L_{1S}^2 + L_{1C}^2} \end{aligned} $$Finally, the outer perimeter defined by the two new small right triangles is twice the value of a single small triangle's hypotneuse, $H_1$.
$$ \begin{aligned} P_1 &= 2 \cdot H_1 \\ &= 2 \cdot \sqrt{L_{1S}^2 + L_{1C}^2} \end{aligned} $$3.3 Analysis at n = 2 and above¶
As the index increases, the efforts in the above are repeated. $2^{n+1}$ right triangles are created, of which half are $T_{nB}$ and half are $T_{nS}$. Any $T_{nB}$ will have a leg that's shared with a $T_{nS}$ called $L_{nC}$. This common leg is exactly half the hypotneuse from the previous iteration. Using this information one can solve for $L_{nB}$, $L_{nS}$, and $H_n$.
$$ \begin{aligned} L_{nC} &= \frac{H_{n-1}}{2} \\ L_{nB} &= \sqrt{r^2 - L_{nC}^2} \\ L_{nS} &= r - L_{nB} \end{aligned} $$With the legs of $T_{nS}$ known, one can find the hypotneuse of $T_{nS}$ using the Pythagorean theorem.
$$ \begin{aligned} H_n &= \sqrt{L_{nS}^2 + L_{nC}^2} \\ &= \sqrt{\left(r - \sqrt{r^2 - \left(\frac{H_{n-1}}{2}\right)^2}\right)^2 + \left(\frac{H_{n-1}}{2}\right)^2} \end{aligned} $$The above is a recurrence relation for $H_n$ for all $n > 0$. The initial value derived above, $H_0$, is just $\sqrt{2} \cdot r$. The perimeter at an arbitrary index is comprised of $2^n$ right triangles' hypotneuses.
$$ \begin{aligned} P_n &= 2^n \cdot H_n \\ &= 2^n \cdot \sqrt{\left(r - \sqrt{r^2 - \frac{H_{n-1}^2}{4}}\right)^2 + \frac{H_{n-1}^2}{4}} \end{aligned} $$Below are plots for $n = 2$ and $n = 3$. Only $T_n$ and $T_{n-1}$ are drawn to reduce graphical clutter. The new iteration's triangles become more difficult to see as the index increases so plots of $n \geq 4$ are not shown.
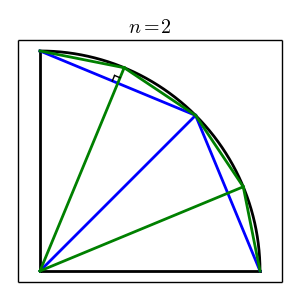
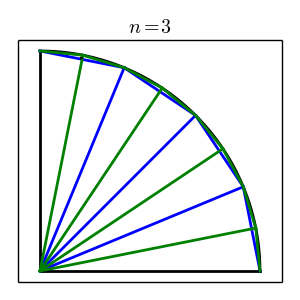
4.0 Computing $\pi$¶
The circumference of the circle is approximated by $4 \cdot P_n$, where the factor of four is present since we only considered the region between $0$ and $90$ degrees (all other regions are identical). The quantity $4 \cdot P_n$ will always be slightly smaller than the true circumference but would converge in the limit as $n \rightarrow \infty$. Equating $4 \cdot P_n$ with the true circumference, $\pi \cdot 2 \cdot r$, and solving for $\pi$ yields:
$$ \begin{aligned} \pi &= \lim_{n\rightarrow\infty} \frac{2 \cdot P_n}{r} \end{aligned} $$Since computing something to infinity is not possible, let's accept that we're stuck with an approximation and recognize it using $\approx$ in the below expression for $\pi$. These equations are readily implemented in code with a for loop and can be evaluated for as large an $n$ that our computing resources will permit.
The downside to this approach is that as $n$ increases, $H_n$ gets smaller and smaller. For example, consider the unit circle with $r = 1$. As $n$ increases, the above equation presents a precision challenge for any computer since it involves the difference of a constant (unity) with an ever-decreasing quantity ($H_{n-1}^2/4$) that approaches zero as $n \rightarrow \infty$.
4.1 In terms of incremental area¶
It is also possible to use the triangles' areas to compute $\pi$. The additional area contributed by each iteration can be computed by analyzing $T_{nS}$, the area of which is written below by using the Pythagorean theorem for $L_{nS}$.
$$ \begin{aligned} A_{TnS} &= \frac{1}{2} \cdot L_{nC} \cdot L_{nS} \\ &= \frac{1}{2} \cdot \frac{H_{n-1}}{2} \cdot \sqrt{H_n^2 - \left( \frac{H_{n-1}}{2} \right)^2} \\ &= \frac{H_{n-1}}{4} \cdot \left(r - \sqrt{r^2 - \left( \frac{H_{n-1}}{2} \right)^2} \right) \end{aligned} $$There are $2^n$ such $T_{nS}$ in the region between $0$ and $90$ degrees. Therefore, multiplying $A_{TnS}$ by $2^{n+2}$ gives the total incremental area at an arbitrary index, $\Delta A_n$.
$$ \begin{aligned} \Delta A_n &= 2^{n+2} \cdot A_{TnS} \\ &= 2^n \cdot H_{n-1} \cdot \left(r - \sqrt{r^2 - \left( \frac{H_{n-1}}{2} \right)^2} \right) \end{aligned} $$The total area at some index, $A_n$, is an accumulation of $\Delta A_n$ plus the initial value, $A_0$.
$$ \begin{aligned} A_0 &= 2 \cdot r^2 \\ A_n &= A_0 + \sum_n \Delta A_n \mbox{ , for } n>0 \end{aligned} $$As for the perimeter case, if the area-based result is used to compute $\pi$ then it is at best an approximation. When implemented in code it has the same precision limitations as the perimeter case.
$$ \begin{aligned} \pi &\approx \frac{A_n}{r^2} \end{aligned} $$5.0 Python implementation¶
from math import sqrt
# http://www.piday.org/million/
PI = '3.141592653589793238462643383279502884197169399375' # and many more ...
def compare_pi(value):
"""
Compare the approximation to pi given by 'value' to the actual value.
- 'value' argument must be a float
"""
# first, convert 'value' into a super-long string
value = '%.050g' % value
# next, iterate over the characters in the PI string
# if there is a mismatch between PI and value, stop iterating
for i in xrange(len(PI)):
if PI[i] != value[i]:
print 'correct portion = %s' % value[0:i]
# the conditional ignores each string's decimal symbol
print 'mismatch at digit %d' % (i if i > 0 else 1)
break
# assign the radius and number of iterations
# make r a float to avoid unintentional integer division
r = 1.0
# in its current form, the best this script can do is 16 decimal places
# this occurs for iterations >= 24
iterations = 24
# during every loop:
# (1) compute the current hypotneuse using the previous hypotneuse
# (2) compute pi using the current hypotneuse
for n in xrange(iterations):
if n == 0:
H_current = sqrt(2) * r
else:
H_current = sqrt(
(r - sqrt(r ** 2 - H_previous ** 2 / 4)) ** 2 +
H_previous ** 2 / 4
)
pi_approximated = 2 ** (n + 1) * H_current / r
H_previous = H_current
# conditional that avoids printing each iteration's details
if n > 1 and n < iterations - 2:
if n in [2, 3, 4]:
print '...'
continue
print '--------------------------------------------------------'
print 'iteration number %d' % (n + 1)
print 'n = {:}, which gives {:,} triangles'.format(n, 2 ** (n + 1))
print 'calculated pi = %.030g' % pi_approximated
compare_pi(pi_approximated)
Download this post's IPython notebook here.
Comments !